initiation cadran solaire

Qu'est ce qu'un cadran solaire ?

Le principe du cadran solaire repose sur la projection de l'ombre d'une tige (appelée style) sur un support gradué. Le Soleil effectuant une révolution apparente toutes les 24 heures (c'est évidemment la Terre qui tourne sur elle-même), il est possible de mesurer l'angle horaire du Soleil et de retrouver l'heure solaire vraie, et par le biais de corrections, l'heure légale.

Il est possible de construire des cadrans sur tout type de support plan ou non. Les cadrans non plans sont assez rares et très difficiles à construire. Les cadrans plans sont aussi variés que l'orientation et l'inclinaison du support. Les plus courants sont les cadrans horizontaux (placés souvent sur des colonnes dans les jardins) et les cadrans verticaux méridionaux (à la façade des maisons et églises).

La science des cadrans solaires s'appelle la gnomonique, à ne pas confondre avec la gnomique en dépit de leur étymologie commune.

Un cadran comporte des lignes et des inscriptions caractéristiques qui ont un sens précis. Voyons cela sur un exemple de cadran vertical méridional

Les lignes droites sont appelées les lignes horaires. Elles permettent de connaître l'heure à partir de l'ombre du style. Certaines lignes donnent l'heure pleine (1), la demi-heure (2) ou le quart d'heure (3) ou màªme toutes les cinq minutes.
Le style est formé de deux parties : le style droit planté en A et le style polaire planté en B. La ligne passant par ces deux points s'appelle la ligne sous-stylaire (5).
La ligne horaire correspondant au midi solaire est la droite de plus grande pente (6). Elle correspond à l'intersection du méridien du lieu avec la table du cadran.
Selon la saison, l'ombre est plus ou moins longue et éloignée du point B, en fonction de la déclinaison du soleil. On repà¨re les moments remarquables comme les solstices (7) et les équinoxes (8). Les autres courbes intermédiaires sont les courbes de déclinaison.

Au delà de l'aspect mesure du temps (qui de toute façon ne peut pas lutter face aux montres modernes), le cadran solaire doit se caractériser par un graphisme et une décoration originale. Le cadran égaye les façades et les jardins et certains cadrans sont de véritables oeuvres d'art.
La devise associée au cadran lui donne sa personnalité. Sur les cadrans modernes, elle est moins souvent en latin mais toujours empreinte de philosophie. Elle peut être tirée d'une oeuvre littéraire ou former une maxime sentencieuse.
Les cadrans verticaux sont souvent peints sur les façades. La région du sud des Alpes en fourmille, dont certains sont trà¨s bien conservés ou restaurés. La technique doit être sà»re pour résister aux outrages du temps. Plus aisé à réaliser, le cadran sur bois ou sur métal a l'avantage de pouvoir être préparé dans un autre lieu que son lieu d'installation.
Quoi qu'il en soit, le cadran solaire est source de plaisirs artistiques, scientifiques et historiques. Le logiciel freeware "Shadows" est là pour prendre en charge l'aspect mathématique et vous permettre de vous concentrer sur l'aspect artistique.

Comment lire l'heure sur un cadran solaire ?

L'heure solaire est suffisante en elle-même, cependant il est intéressant de calculer l'heure légale à partir de l'heure solaire affichée sur le cadran.
Pour cela il faut appliquer en général trois corrections à l'heure solaire affichée sur le cadran pour obtenir l'heure légale:

La correction en longitude.
La correction de l'équation du temps.
L'ajout d'une heure en hiver ou 2 heures en été.

Heure légale = heure du cadran + correction en longitude + correction équation du temps + 1 h en hiver (2 h en été)

Attention, les cadrans solaires intègrent souvent à la construction l'heure d'hiver et la correction en longitude.

Correction en longitude.

le globe terrestre est divisé en 24 fuseaux horaires à l'intérieur desquels l'heure 'légale' reste la même. Dans chaque fuseau horaire la longitude varie de 15° (relativement de - 7.5° à + 7.5° par rapport au centre du fuseau).

360° => 24 heures 15° => 1 heure 1° => 4 minutes

Au centre du fuseau horaire, le temps civil (heure légale) est égal au temps solaire moyen. Pour les autres endroits du fuseau il faut faire une correction en longitude de 4 minutes par degré de longitude.

Pour la France le centre du fuseau horaire est celui de Greenwich (0° de longitude), Nice est à une longitude de 7° 15' Est par rapport au centre du fuseau, ce qui donne une correction de 29 minutes. Le Soleil se là¨ve et se couche 29 minutes plus tà´t à Nice qu'à Greenwich.

Exemple de correction en longitude:

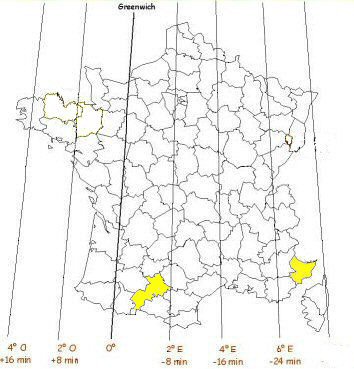
Longitude du lieu	Décalage de longitude en minutes et secondes	Remarque
7° 12 Est	-28 mn 48 s	Le soleil arrivera à Greenwich plus tard
1° 45 Ouest	+7 mn	Le soleil est déjà passé à Greenwich
7° 15' Est	-29 mn	Le soleil arrivera à Greenwich plus tard
1° 30 Est	-6 mn	Le soleil arrivera à Greenwich plus tard

Un autre exemple, Montréal au Canada, se trouve à une longitude de 73,5º ouest, soit 1,5º à l'est du centre du fuseau (75°), ce qui donne une correction de 6 minutes. Le Soleil se là¨ve et se couche 6 minutes plus tà´t à Montréal qu'au centre du fuseau horaire.

Correction de l'équation du temps.

La rotation de la terre sur elle-même sur un axe incliné et sa trajectoire elliptique autour du soleil font que la durée entre deux passages du soleil au méridien local n'est pas constante.

Les légà¨res différences de durée journalià¨re (inférieures à 30 secondes) entre le midi moyen (temps civil local) et le midi vrai (au Soleil) s'accumulent et le décalage peut s'annuler ou atteindre un maximum de plus ou moins 16 minutes. La conséquence essentielle est qu'au cours de l'année, l'instant du passage du Soleil au méridien (le midi solaire) se décale lentement jour aprà¨s jour par rapport au midi indiqué par une horloge parfaitement réglée.

Ces deux particularités du mouvement de la terre autour du soleil:

axe de rotation de la Terre n'est pas perpendiculaire au plan de son orbite, mais incliné
orbite n'est pas un cercle, mais une ellipse dont le Soleil occupe un des foyers

font que la durée d'une heure solaire n'est pas constante au cours de l'année et que ces imperfections doivent être corrigés par l'équation du temps.

La figure ci-dessous représente la courbe de l'équation du temps (en rouge), somme de l'équation de l'Ellipticité (en bleu) et de l'obliquité (en vert). Elle indique la différence entre le Soleil « vrai » indiqué par le cadran et un Soleil « moyen » donné une horloge parfaitement réglée.

L'équation du temps s'annule quatre fois par an, aux environs du 15 avril, 13 juin, 1 septembre et 25 décembre. Elle atteint son minimum (-16 minutes 28 secondes) le 5 novembre et son maximum (14 minutes 15 secondes) le 11 février. Cette courbe est valable pour 200 ans à quelques secondes prà¨s.

Par rapport à l'heure solaire "vraie" qui vaut midi lorsque le soleil passe au méridien, il faut opérer la correction indiquée par l'équation du temps pour obtenir l'heure "du temps civil local".
Autrement dit, pour passer de l'heure lue sur un cadran solaire à l'heure solaire moyenne (heure civile), il faut appliquer la correction de l'équation du temps.

Exemples de correction :

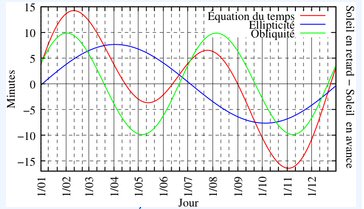
1 février	+ 13 mn	15 avril	0 mn
5 aoà»t	+ 06 mn	13 juin	0 mn
16 septembre	- 04 mn	1 septembre	0 mn
1 octobre	- 10 mn	25 décembre	0 mn
11 février	+ 14mn	5 novembre	- 16 mn

Donc l'heure légale s'obtient en ajoutant à l'heure du cadran les différentes corrections vues ci-dessus.

Heure légale = heure du cadran + correction en longitude + correction équation du temps + 1 h en hiver (2 h en été)

L'exemple ci-dessous indique les corrections à appliquer à un cadran situé à 44°10' Nord et 7° 12' Est:

Le 29 juillet 2010	Temps
Heure solaire	12h00 (midi)
correction 1 - Longitude Correction 2 - à‰quation du temps Correction 3 - heure d'été	-28mn 48s +6mn 28s 2h
Heure légale	13h 37mn 40s

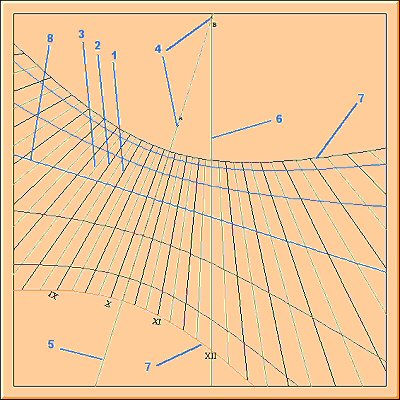
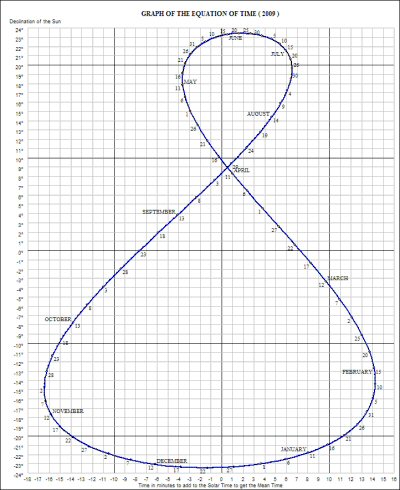
Autre forme de la courbe de l'équation du temps - Verticale ou huit
Le graphe représente ici la déclinaison du soleil (en ordonnées) en fonction de la variante du temps en minutes (en abscisse).
La courbe représente un grand huit fermé qui s'obtient en repliant la courbe de l'équation du temps exprimée en fonction de la date.

REMARQUE: Pour simplifier la lecture de l'heure solaire, les cadrans que vous trouverez sur ce site, tiennent compte de l'heure d'hiver (TU+1H) et du décalage horaire dà» à la longitude du lieu (-28mn 48s).

Sur le cadran vertical déclinant, pour connaà®tre l'heure légale il faut ajouter à l'heure solaire, la correction de l'équation du temps et une heure en été.
Sur les cadrans équatoriaux, il suffit seulement d'appliquer la correction de l'équation du temps.